本文在Python中用箱線圖、傅里葉變換、熵、自相關(guān)和 PCA 分析時間序列數(shù)據(jù)。數(shù)據(jù)可視化是任何數(shù)據(jù)相關(guān)項目中最重要的階段之一。根據(jù)數(shù)據(jù)可視化的對象，有：

　　1.數(shù)據(jù)可視化報告結(jié)果。

　　2.數(shù)據(jù)可視化來分析數(shù)據(jù)，換句話說，數(shù)據(jù)科學家內(nèi)部使用的可視化來提取有關(guān)數(shù)據(jù)的信息，然后實施模型。

　　本文主要關(guān)注后一種，因為它解釋了一些有助于分析時間序列數(shù)據(jù)的方法。

　　什么是時間序列?

　　基本數(shù)值時間序列是有序的、帶時間戳的觀測值(測量值)的集合，其中每個觀測值都是從同一測量過程中獲得的數(shù)值標量。

　　什么是時間戳?

　　在我們將“時間”捕獲為數(shù)據(jù)點之前，我們不會深入探討需要精確定義的許多細節(jié)(準確性、格式、日歷約定、時區(qū)等等)。我們將時間戳定義為具有所需精度的時間點的表示就足夠了。例如，這可能是根據(jù)某個日歷的日期約定(例如“08-06-2020”)，或者自 1970 年以來以整數(shù)表示的毫秒數(shù)(這實際上是 UNIX 紀元約定!)

　　Python類庫

　　首先，這些是與 notebook 一起使用的庫。大多數(shù)代碼都圍繞 NumPy 和 Pandas庫，因為數(shù)據(jù)主要以 Pandas Dataframe 表現(xiàn)的 NumPy 數(shù)組。

　　導入文件

　　下載數(shù)據(jù)后，運行以下代碼將其導入。

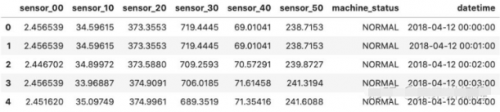
　　正如所觀察到的，數(shù)據(jù)包含六個傳感器的傳感器數(shù)據(jù)、每個數(shù)據(jù)點的日期時間以及機器狀態(tài)。這是“BROKEN”、“NORMAL”或“RECOVERING”，但為了簡化可視化，它被分組如下：

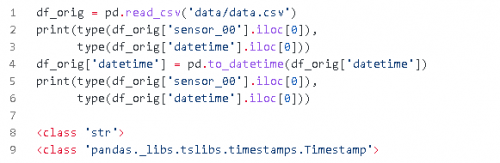
　　在任何編程語言中使用日期時間總是具有挑戰(zhàn)性的，Python 也不例外。盡管處理日期時間有多種方法，但這里使用函數(shù) pandas.to_datetime 將 datetime 列(讀取為字符串)轉(zhuǎn)換為時間戳。

　　數(shù)據(jù)預處理

　　在進行可視化之前，分析了本次數(shù)據(jù)的重復值和缺失值。并且刪除重復項的函數(shù)：

　　填充缺失值的函數(shù)：

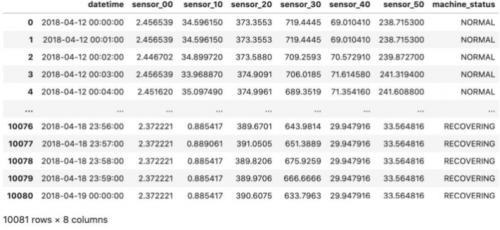
　　這是預處理階段的整個管道。此外，數(shù)據(jù)分為輸入數(shù)據(jù)和輸出數(shù)據(jù)。

　　輸入形狀：(10081, 7)

　　輸出形狀：(10081, 2)

　　數(shù)據(jù)可視化

　　現(xiàn)在，準備開始數(shù)據(jù)可視化。這是傳感器數(shù)據(jù)和異常情況的圖。完整代碼可以在公眾號:機器學習研習院 后臺回復 時間序列可視化 獲取.

　　均值和標準

　　可以更好地總結(jié)數(shù)據(jù)隨時間變化的行為的最基本圖之一是均值標準圖，我們在其中顯示按時間范圍分組的均值和標準差。這主要有助于分析指定時間范圍內(nèi)的基線和噪聲。

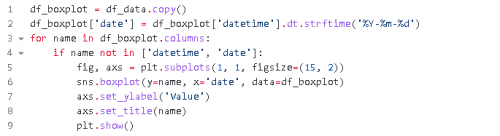
　　箱形圖

　　另一個有趣的圖表是通過箱線圖顯示的。箱線圖是一種通過四分位數(shù)以圖形方式顯示數(shù)值數(shù)據(jù)的局部性、擴散性和偏度組的方法。有兩個主要框表示從第25個百分位數(shù)到第75個百分位數(shù)的數(shù)據(jù)，兩者之間用分布的中位數(shù)隔開。除了盒子之外，還有從盒子延伸出來的晶須，表明上四分位和下四分位之外的變異性。與數(shù)據(jù)集其他部分顯著不同的異常值也被繪制為箱線圖上須之外的單獨點。

　　這一個類似于平均和標準圖，因為它表明數(shù)據(jù)的平穩(wěn)性。但是，它也可以顯示異常值，這有助于從視覺上檢測異常和數(shù)據(jù)之間的任何關(guān)系。

　　傅里葉變換

　　快速傅里葉變換(FFT)是一種計算序列離散傅里葉變換的算法。這種類型的圖很有趣，因為它是處理時間序列時特征提取的主要方法之一。通常的做法不是用時間序列來訓練模型，而是應用傅里葉變換來提取頻率，然后訓練模型。

　　為此，我們必須選擇一個滑動窗口來計算FFT。滑動窗口越寬，頻率數(shù)越高。缺點是您將得到更少的時間戳，從而丟失數(shù)據(jù)的時間分辨率。當減小窗口的大小時，我們得到了相反的結(jié)果：更少的頻率但更高的時間分辨率。然后，窗口的大小應該取決于任務。

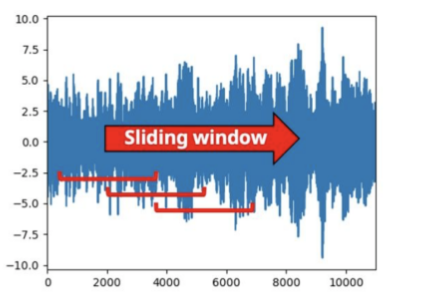
　　FFT的滑動窗口 對于如下圖所示，我選擇了一個包含64個數(shù)據(jù)的時間窗口。因此，頻率從1 - 32hz。

　　熵

　　可視化信息和熵是機器學習中的一個有用工具，因為它們是許多特征選擇、構(gòu)建決策樹和擬合分類模型的基礎。

　　熵的計算如下：

　　歸一化頻率分布

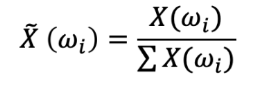
　　計算熵

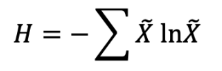
　　最低熵是針對某一隨機變量計算的，該隨機變量的單個事件的概率為1.0，即確定性。一個隨機變量的最大熵是當所有事件都是等可能的。

　　降維

　　當有多個傳感器時，實現(xiàn)一種降維方法來獲得包含大部分信息的1、2或3個主要組件總是很有趣的。

　　對于這個例子，我實現(xiàn)了主成分分析(PCA)。這是計算主要組件并使用它們對數(shù)據(jù)進行基礎更改的過程。

　　被解釋方差比率是每一個被選擇的組成部分的方差百分比。

　　對于第一個PCA組件，可以繪制數(shù)據(jù)，并直觀地檢查異常和時間序列之間是否存在關(guān)系。

　　自相關(guān)

　　最后，特別是對于預測任務，繪制數(shù)據(jù)的自相關(guān)性是很有趣的。這個表示給定的時間序列和它自己在連續(xù)時間間隔中的滯后版本之間的相似程度。

　　與自相關(guān)相關(guān)的是增強迪基-富勒統(tǒng)計檢驗，用于檢驗給定的時間序列是否平穩(wěn)。