網絡是由一些緊密相連的節點組成的，并且根據不同節點之間連接的緊密程度，網絡也可視為由不同簇組成。簇內的節點之間有著更為緊密的連接，不同簇之間的連接則相對稀疏。這種簇被稱為網絡中的社區結構(community structure)。

　　由此衍生出來的社區發現(community detection)算法用來發現網絡中的社區結構，這類算法包括 Louvain 算法、Girvan-Newman 算法以及 Bron-Kerbosch 算法等。

　　最近，在 GitHub 上發現了一個可以發現圖中社區結構的 Python 庫 communities，該庫由軟件工程師 Jonathan Shobrook 創建。

　　項目地址：https://github.com/shobrook/communities

　　首先，該庫可以實現以下幾種社區發現算法：

　　Louvain 算法

　　Girvan-Newman 算法

　　層次聚類

　　譜聚類

　　Bron-Kerbosch 算法

　　其次，用戶還可以使用 communities 庫來可視化上述幾種算法。

　　該庫的安裝方法也非常簡單，可采用 pip 的方式安裝 communities，代碼如下：

　　對于這個 Python 庫，很多網友給予了高度評價，表示會去嘗試。

　　算法詳解

　　1、Louvain 算法

　　該算法來源于文章《Fast unfolding of communities in large networks》，簡稱為 Louvian。

　　作為一種基于模塊度(Modularity)的社區發現算法，Louvain 算法在效率和效果上都表現比較好，并且能夠發現層次性的社區結構，其優化的目標是最大化整個圖屬性結構(社區網絡)的模塊度。

　　Louvain 算法對最大化圖模塊性的社區進行貪婪搜索。如果一個圖具有高密度的群體內邊緣和低密度的群體間邊緣，則稱之為模圖。

　　示例代碼如下：

　　2、Girvan-Newman 算法

　　該算法來源于文章《Community structure in social and biological networks》。

　　Girvan-Newman 算法迭代刪除邊以創建更多連接的組件。每個組件都被視為一個 community，當模塊度不能再增加時，算法停止去除邊緣。

　　示例代碼如下：

　　3、層次聚類

　　層次聚類實現了一種自底向上、分層的聚類算法。每個節點從自己 的社區開始，然后，隨著層次結構的建立，最相似的社區被合并。社區會一直被合并，直到在模塊度方面沒有進一步的進展。

　　示例代碼如下：

　　4、譜聚類

　　這種類型的算法假定鄰接矩陣的特征值包含有關社區結構的信息。

　　示例代碼如下：

　　5、Bron-Kerbosch 算法

　　Bron-Kerbosch 算法實現用于最大團檢測(maximal clique detection)。圖中的最大團是形成一個完整圖的節點子集，如果向該子集中添加其他節點，則它將不再完整。將最大團視為社區是合理的，因為團是圖中連接最緊密的節點群。因為一個節點可以是多個社區的成員，所以該算法有時會識別重疊的社區。

　　示例代碼如下：

　　可視化

　　繪圖

　　可視化圖(graph)，將節點分組至它們所屬的社區和顏色編碼中。返回代表繪圖的 matplotlib.axes.Axes。示例代碼如下：

　　可視化圖如下：

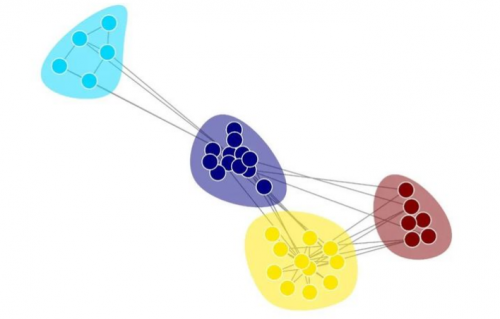
　　Louvain 算法的動圖展示

　　Louvain 算法在圖中的應用可以實現動圖展示，其中每個節點的顏色代表其所屬的社區，并且同一社區中的節點聚類結合在一起。

　　示例代碼如下：