排序算法是《數(shù)據(jù)結(jié)構(gòu)與算法》中最基本的算法之一。本文介紹10種常見的內(nèi)部排序算法，及如何用Python實(shí)現(xiàn)。

　　排序算法可以分為內(nèi)部排序和外部排序，內(nèi)部排序是數(shù)據(jù)記錄在內(nèi)存中進(jìn)行排序，而外部排序是因排序的數(shù)據(jù)很大，一次不能容納全部的排序記錄，在排序過(guò)程中需要訪問(wèn)外存。

　　常見的內(nèi)部排序算法有：插入排序、希爾排序、選擇排序、冒泡排序、歸并排序、快速排序、堆排序、基數(shù)排序等。

　　用一張圖概括：

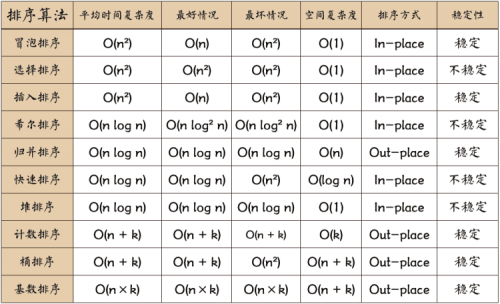
　　關(guān)于時(shí)間復(fù)雜度：

　　●平方階 (O(n2)) 排序：各類簡(jiǎn)單排序，直接插入、直接選擇和冒泡排序;

　　●線性對(duì)數(shù)階 (O(nlog2n)) 排序：快速排序、堆排序和歸并排序;

　　●希爾排序：O(n1+§)) 排序，§ 是介于 0 和 1 之間的常數(shù);

　　●線性階 (O(n)) 排序：基數(shù)排序，此外還有桶、箱排序。

　　關(guān)于穩(wěn)定性：

　　●排序后 2 個(gè)相等鍵值的順序和排序之前它們的順序相同。

　　●穩(wěn)定的排序算法：冒泡排序、插入排序、歸并排序和基數(shù)排序。

　　●不是穩(wěn)定的排序算法：選擇排序、快速排序、希爾排序、堆排序。

　　名詞解釋：

　　●n：數(shù)據(jù)規(guī)模。

　　●k：“桶”的個(gè)數(shù)。

　　●In-place：占用常數(shù)內(nèi)存，不占用額外內(nèi)存。

　　●Out-place：占用額外內(nèi)存。

　　冒泡排序

　　冒泡排序(Bubble Sort)也是一種簡(jiǎn)單直觀的排序算法。它重復(fù)地走訪過(guò)要排序的數(shù)列，一次比較兩個(gè)元素，如果他們的順序錯(cuò)誤就把他們交換過(guò)來(lái)。走訪數(shù)列的工作是重復(fù)地進(jìn)行直到?jīng)]有再需要交換，也就是說(shuō)該數(shù)列已經(jīng)排序完成。這個(gè)算法的名字由來(lái)是因?yàn)樵叫〉脑貢?huì)經(jīng)由交換慢慢“浮”到數(shù)列的頂端。

　　作為最簡(jiǎn)單的排序算法之一，冒泡排序給我的感覺(jué)就像 Abandon 在單詞書里出現(xiàn)的感覺(jué)一樣，每次都在第一頁(yè)第一位，所以最熟悉。冒泡排序還有一種優(yōu)化算法，就是立一個(gè) flag，當(dāng)在一趟序列遍歷中元素沒(méi)有發(fā)生交換，則證明該序列已經(jīng)有序。但這種改進(jìn)對(duì)于提升性能來(lái)說(shuō)并沒(méi)有什么太大作用。

　　1.算法步驟

　　●比較相鄰的元素。如果第一個(gè)比第二個(gè)大，就交換他們兩個(gè)。

　　●對(duì)每一對(duì)相鄰元素作同樣的工作，從開始第一對(duì)到結(jié)尾的最后一對(duì)。這步做完后，最后的元素會(huì)是最大的數(shù)。

　　●針對(duì)所有的元素重復(fù)以上的步驟，除了最后一個(gè)。

　　●持續(xù)每次對(duì)越來(lái)越少的元素重復(fù)上面的步驟，直到?jīng)]有任何一對(duì)數(shù)字需要比較。

　　2.Python 代碼

　　def bubbleSort(arr):

　　for i in range(1, len(arr)):

　　for j in range(0, len(arr)-i):

　　if arr[j] > arr[j+1]:

　　arr[j], arr[j + 1] = arr[j + 1], arr[j]

　　return arr

　　選擇排序

　　選擇排序是一種簡(jiǎn)單直觀的排序算法，無(wú)論什么數(shù)據(jù)進(jìn)去都是 O(n²) 的時(shí)間復(fù)雜度。所以用到它的時(shí)候，數(shù)據(jù)規(guī)模越小越好。唯一的好處可能就是不占用額外的內(nèi)存空間了吧。

　　1.算法步驟

　　●首先在未排序序列中找到最小(大)元素，存放到排序序列的起始位置。

　　●再?gòu)氖Ｓ辔磁判蛟刂欣^續(xù)尋找最小(大)元素，然后放到已排序序列的末尾。

　　●重復(fù)第二步，直到所有元素均排序完畢。

　　2.Python 代碼

　　def selectionSort(arr):

　　for i in range(len(arr) - 1):

　　# 記錄最小數(shù)的索引

　　minIndex = i

　　for j in range(i + 1, len(arr)):

　　if arr[j] < arr[minIndex]:

　　minIndex = j

　　# i 不是最小數(shù)時(shí)，將 i 和最小數(shù)進(jìn)行交換

　　if i != minIndex:

　　arr[i], arr[minIndex] = arr[minIndex], arr[i]

　　return arr

　　插入排序

　　插入排序的代碼實(shí)現(xiàn)雖然沒(méi)有冒泡排序和選擇排序那么簡(jiǎn)單粗暴，但它的原理應(yīng)該是最容易理解的了，因?yàn)橹灰蜻^(guò)撲克牌的人都應(yīng)該能夠秒懂。插入排序是一種最簡(jiǎn)單直觀的排序算法，它的工作原理是通過(guò)構(gòu)建有序序列，對(duì)于未排序數(shù)據(jù)，在已排序序列中從后向前掃描，找到相應(yīng)位置并插入。

　　插入排序和冒泡排序一樣，也有一種優(yōu)化算法，叫做拆半插入。

　　1.算法步驟

　　●將第一待排序序列第一個(gè)元素看做一個(gè)有序序列，把第二個(gè)元素到最后一個(gè)元素當(dāng)成是未排序序列。

　　●從頭到尾依次掃描未排序序列，將掃描到的每個(gè)元素插入有序序列的適當(dāng)位置。(如果待插入的元素與有序序列中的某個(gè)元素相等，則將待插入元素插入到相等元素的后面。)

　　2.Python 代碼

　　def insertionSort(arr):

　　for i in range(len(arr)):

　　preIndex = i-1

　　current = arr[i]

　　while preIndex >= 0 and arr[preIndex] > current:

　　arr[preIndex+1] = arr[preIndex]

　　preIndex-=1

　　arr[preIndex+1] = current

　　return arr

　　希爾排序

　　希爾排序，也稱遞減增量排序算法，是插入排序的一種更高效的改進(jìn)版本。但希爾排序是非穩(wěn)定排序算法。

　　希爾排序是基于插入排序的以下兩點(diǎn)性質(zhì)而提出改進(jìn)方法的：

　　●插入排序在對(duì)幾乎已經(jīng)排好序的數(shù)據(jù)操作時(shí)，效率高，即可以達(dá)到線性排序的效率;

　　●但插入排序一般來(lái)說(shuō)是低效的，因?yàn)椴迦肱判蛎看沃荒軐?shù)據(jù)移動(dòng)一位。

　　希爾排序的基本思想是：先將整個(gè)待排序的記錄序列分割成為若干子序列分別進(jìn)行直接插入排序，待整個(gè)序列中的記錄“基本有序”時(shí)，再對(duì)全體記錄進(jìn)行依次直接插入排序。

　　1.算法步驟

　　●選擇一個(gè)增量序列 t1，t2，……，tk，其中 ti > tj, tk = 1;

　　●按增量序列個(gè)數(shù) k，對(duì)序列進(jìn)行 k 趟排序;

　　●每趟排序，根據(jù)對(duì)應(yīng)的增量 ti，將待排序列分割成若干長(zhǎng)度為 m 的子序列，分別對(duì)各子表進(jìn)行直接插入排序。僅增量因子為 1 時(shí)，整個(gè)序列作為一個(gè)表來(lái)處理，表長(zhǎng)度即為整個(gè)序列的長(zhǎng)度。

　　2.Python 代碼

　　def shellSort(arr):

　　import math

　　gap=1

　　while(gap < len(arr)/3):

　　gap = gap*3+1

　　while gap > 0:

　　for i in range(gap,len(arr)):

　　temp = arr[i]

　　j = i-gap

　　while j >=0 and arr[j] > temp:

　　arr[j+gap]=arr[j]

　　j-=gap

　　arr[j+gap] = temp

　　gap = math.floor(gap/3)

　　return arr

　　}

　　歸并排序

　　歸并排序(Merge sort)是建立在歸并操作上的一種有效的排序算法。該算法是采用分治法(Divide and Conquer)的一個(gè)非常典型的應(yīng)用。

　　作為一種典型的分而治之思想的算法應(yīng)用，歸并排序的實(shí)現(xiàn)由兩種方法：

　　●自上而下的遞歸(所有遞歸的方法都可以用迭代重寫，所以就有了第 2 種方法);

　　●自下而上的迭代。

　　和選擇排序一樣，歸并排序的性能不受輸入數(shù)據(jù)的影響，但表現(xiàn)比選擇排序好的多，因?yàn)槭冀K都是 O(nlogn) 的時(shí)間復(fù)雜度。代價(jià)是需要額外的內(nèi)存空間。

　　1.算法步驟

　　●申請(qǐng)空間，使其大小為兩個(gè)已經(jīng)排序序列之和，該空間用來(lái)存放合并后的序列;

　　●設(shè)定兩個(gè)指針，最初位置分別為兩個(gè)已經(jīng)排序序列的起始位置;

　　●比較兩個(gè)指針?biāo)赶虻脑兀x擇相對(duì)小的元素放入到合并空間，并移動(dòng)指針到下一位置;

　　●重復(fù)步驟 3 直到某一指針達(dá)到序列尾;

　　●將另一序列剩下的所有元素直接復(fù)制到合并序列尾。

　　2.Python 代碼

　　def mergeSort(arr):

　　import math

　　if(len(arr)<2):

　　return arr

　　middle = math.floor(len(arr)/2)

　　left, right = arr[0:middle], arr[middle:]

　　return merge(mergeSort(left), mergeSort(right))

　　def merge(left,right):

　　result = []

　　while left and right:

　　if left[0] <= right[0]:

　　result.append(left.pop(0));

　　else:

　　result.append(right.pop(0));

　　while left:

　　result.append(left.pop(0));

　　while right:

　　result.append(right.pop(0));

　　return result

　　快速排序

　　快速排序是由東尼·霍爾所發(fā)展的一種排序算法。在平均狀況下，排序 n 個(gè)項(xiàng)目要 Ο(nlogn) 次比較。在最壞狀況下則需要 Ο(n2) 次比較，但這種狀況并不常見。事實(shí)上，快速排序通常明顯比其他 Ο(nlogn) 算法更快，因?yàn)樗膬?nèi)部循環(huán)(inner loop)可以在大部分的架構(gòu)上很有效率地被實(shí)現(xiàn)出來(lái)。

　　快速排序使用分治法(Divide and conquer)策略來(lái)把一個(gè)串行(list)分為兩個(gè)子串行(sub-lists)。

　　快速排序又是一種分而治之思想在排序算法上的典型應(yīng)用。本質(zhì)上來(lái)看，快速排序應(yīng)該算是在冒泡排序基礎(chǔ)上的遞歸分治法。

　　快速排序的名字起的是簡(jiǎn)單粗暴，因?yàn)橐宦牭竭@個(gè)名字你就知道它存在的意義，就是快，而且效率高!它是處理大數(shù)據(jù)最快的排序算法之一了。

　　雖然 Worst Case 的時(shí)間復(fù)雜度達(dá)到了 O(n²)，但是人家就是優(yōu)秀，在大多數(shù)情況下都比平均時(shí)間復(fù)雜度為 O(n logn) 的排序算法表現(xiàn)要更好，可是這是為什么呢，我也不知道。好在我的強(qiáng)迫癥又犯了，查了 N 多資料終于在《算法藝術(shù)與信息學(xué)競(jìng)賽》上找到了滿意的答案：

　　快速排序的最壞運(yùn)行情況是 O(n²)，比如說(shuō)順序數(shù)列的快排。但它的平攤期望時(shí)間是 O(nlogn)，且 O(nlogn) 記號(hào)中隱含的常數(shù)因子很小，比復(fù)雜度穩(wěn)定等于 O(nlogn) 的歸并排序要小很多。所以，對(duì)絕大多數(shù)順序性較弱的隨機(jī)數(shù)列而言，快速排序總是優(yōu)于歸并排序。

　　1.算法步驟

　　●從數(shù)列中挑出一個(gè)元素，稱為 “基準(zhǔn)”(pivot);

　　●重新排序數(shù)列，所有元素比基準(zhǔn)值小的擺放在基準(zhǔn)前面，所有元素比基準(zhǔn)值大的擺在基準(zhǔn)的后面(相同的數(shù)可以到任一邊)。在這個(gè)分區(qū)退出之后，該基準(zhǔn)就處于數(shù)列的中間位置。這個(gè)稱為分區(qū)(partition)操作;

　　●遞歸地(recursive)把小于基準(zhǔn)值元素的子數(shù)列和大于基準(zhǔn)值元素的子數(shù)列排序。

　　遞歸的最底部情形，是數(shù)列的大小是零或一，也就是永遠(yuǎn)都已經(jīng)被排序好了。雖然一直遞歸下去，但是這個(gè)算法總會(huì)退出，因?yàn)樵诿看蔚牡?iteration)中，它至少會(huì)把一個(gè)元素?cái)[到它最后的位置去。

　　2.Python 代碼

　　def quickSort(arr, left=None, right=None):

　　left = 0 if not isinstance(left,(int, float)) else left

　　right = len(arr)-1 if not isinstance(right,(int, float)) else right

　　if left < right:

　　partitionIndex = partition(arr, left, right)

　　quickSort(arr, left, partitionIndex-1)

　　quickSort(arr, partitionIndex+1, right)

　　return arr

　　def partition(arr, left, right):

　　pivot = left

　　index = pivot+1

　　i = index

　　while i <= right:

　　if arr[i] < arr[pivot]:

　　swap(arr, i, index)

　　index+=1

　　i+=1

　　swap(arr,pivot,index-1)

　　return index-1

　　def swap(arr, i, j):

　　arr[i], arr[j] = arr[j], arr[i]

　　堆排序

　　堆排序(Heapsort)是指利用堆這種數(shù)據(jù)結(jié)構(gòu)所設(shè)計(jì)的一種排序算法。堆積是一個(gè)近似完全二叉樹的結(jié)構(gòu)，并同時(shí)滿足堆積的性質(zhì)：即子結(jié)點(diǎn)的鍵值或索引總是小于(或者大于)它的父節(jié)點(diǎn)。堆排序可以說(shuō)是一種利用堆的概念來(lái)排序的選擇排序。分為兩種方法：

　　●大頂堆：每個(gè)節(jié)點(diǎn)的值都大于或等于其子節(jié)點(diǎn)的值，在堆排序算法中用于升序排列;

　　●小頂堆：每個(gè)節(jié)點(diǎn)的值都小于或等于其子節(jié)點(diǎn)的值，在堆排序算法中用于降序排列。

　　堆排序的平均時(shí)間復(fù)雜度為 Ο(nlogn)。

　　1.算法步驟

　　●創(chuàng)建一個(gè)堆 H[0……n-1];

　　●把堆首(最大值)和堆尾互換;

　　●把堆的尺寸縮小 1，并調(diào)用 shift_down(0)，目的是把新的數(shù)組頂端數(shù)據(jù)調(diào)整到相應(yīng)位置;

　　●重復(fù)步驟 2，直到堆的尺寸為 1。

　　2.Python 代碼

　　def buildMaxHeap(arr):

　　import math

　　for i in range(math.floor(len(arr)/2),-1,-1):

　　heapify(arr,i)

　　def heapify(arr, i):

　　left = 2*i+1

　　right = 2*i+2

　　largest = i

　　if left < arrLen and arr[left] > arr[largest]:

　　largest = left

　　if right < arrLen and arr[right] > arr[largest]:

　　largest = right

　　if largest != i:

　　swap(arr, i, largest)

　　heapify(arr, largest)

　　def swap(arr, i, j):

　　arr[i], arr[j] = arr[j], arr[i]

　　計(jì)數(shù)排序

　　計(jì)數(shù)排序的核心在于將輸入的數(shù)據(jù)值轉(zhuǎn)化為鍵存儲(chǔ)在額外開辟的數(shù)組空間中。作為一種線性時(shí)間復(fù)雜度的排序，計(jì)數(shù)排序要求輸入的數(shù)據(jù)必須是有確定范圍的整數(shù)。

　　1.Python 代碼

　　def countingSort(arr, maxValue):

　　bucketLen = maxValue+1

　　bucket = [0]*bucketLen

　　sortedIndex =0

　　arrLen = len(arr)

　　for i in range(arrLen):

　　if not bucket[arr[i]]:

　　bucket[arr[i]]=0

　　bucket[arr[i]]+=1

　　for j in range(bucketLen):

　　while bucket[j]>0:

　　arr[sortedIndex] = j

　　sortedIndex+=1

　　bucket[j]-=1

　　return arr

　　桶排序

　　桶排序是計(jì)數(shù)排序的升級(jí)版。它利用了函數(shù)的映射關(guān)系，高效與否的關(guān)鍵就在于這個(gè)映射函數(shù)的確定。為了使桶排序更加高效，我們需要做到這兩點(diǎn)：

　　●在額外空間充足的情況下，盡量增大桶的數(shù)量。

　　●使用的映射函數(shù)能夠?qū)⑤斎氲?N 個(gè)數(shù)據(jù)均勻的分配到 K 個(gè)桶中。

　　同時(shí)，對(duì)于桶中元素的排序，選擇何種比較排序算法對(duì)于性能的影響至關(guān)重要。

　　什么時(shí)候最快

　　當(dāng)輸入的數(shù)據(jù)可以均勻的分配到每一個(gè)桶中。

　　什么時(shí)候最慢

　　當(dāng)輸入的數(shù)據(jù)被分配到了同一個(gè)桶中。

　　Python 代碼

　　def bucket_sort(s):

　　"""桶排序"""

　　min_num = min(s)

　　max_num = max(s)

　　# 桶的大小

　　bucket_range = (max_num-min_num) / len(s)

　　# 桶數(shù)組

　　count_list = [ [] for i in range(len(s) + 1)]

　　# 向桶數(shù)組填數(shù)

　　for i in s:

　　count_list[int((i-min_num)//bucket_range)].append(i)

　　s.clear()

　　# 回填，這里桶內(nèi)部排序直接調(diào)用了sorted

　　for i in count_list:

　　for j in sorted(i):

　　s.append(j)

　　if __name__ == __main__ :

　　a = [3.2,6,8,4,2,6,7,3]

　　bucket_sort(a)

　　print(a) # [2, 3, 3.2, 4, 6, 6, 7, 8]

　　基數(shù)排序

　　基數(shù)排序是一種非比較型整數(shù)排序算法，其原理是將整數(shù)按位數(shù)切割成不同的數(shù)字，然后按每個(gè)位數(shù)分別比較。由于整數(shù)也可以表達(dá)字符串(比如名字或日期)和特定格式的浮點(diǎn)數(shù)，所以基數(shù)排序也不是只能使用于整數(shù)。

　　1.基數(shù)排序 vs 計(jì)數(shù)排序 vs 桶排序

　　基數(shù)排序有兩種方法： 這三種排序算法都利用了桶的概念，但對(duì)桶的使用方法上有明顯差異：

　　●基數(shù)排序：根據(jù)鍵值的每位數(shù)字來(lái)分配桶;

　　●計(jì)數(shù)排序：每個(gè)桶只存儲(chǔ)單一鍵值;

　　●桶排序：每個(gè)桶存儲(chǔ)一定范圍的數(shù)值。

　　2.Python 代碼

　　def RadixSort(list):

　　i = 0 #初始為個(gè)位排序

　　n = 1 #最小的位數(shù)置為1(包含0)

　　max_num = max(list) #得到帶排序數(shù)組中最大數(shù)

　　while max_num > 10**n: #得到最大數(shù)是幾位數(shù)

　　n += 1

　　while i < n:

　　bucket = {} #用字典構(gòu)建桶

　　for x in range(10):

　　bucket.setdefault(x, []) #將每個(gè)桶置空

　　for x in list: #對(duì)每一位進(jìn)行排序

　　radix =int((x / (10**i)) % 10) #得到每位的基數(shù)

　　bucket[radix].append(x) #將對(duì)應(yīng)的數(shù)

　　組元素加入到相 #應(yīng)位基數(shù)的桶中

　　j = 0

　　for k in range(10):

　　if len(bucket[k]) != 0: #若桶不為空

　　for y in bucket[k]: #將該桶中每個(gè)元素

　　list[j] = y #放回到數(shù)組中

　　j += 1

　　i += 1

　　return list