全文大約【4000】字,不說廢話,只講可以讓你學到技術、明白原理的純干貨!本文帶有豐富的案例及配圖視頻,讓你更好地理解和運用文中的技術概念,并可以給你帶來具有足夠啟迪的思考......
一. Set集合簡介
1.Set定義
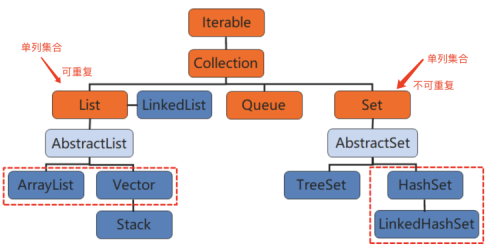
Set是Java的一種集合,繼承自Collection接口,主要有兩個常用的實現類HashSet類和TreeSet類。它沒有固定的大小限制,可以動態地添加和刪除元素。并且Set集合中的元素都是唯一的,不會有重復的元素,即使是null值也只能有一個。另外Set集合是無序的,不能記住元素的添加順序,因為沒有索引值,所以Set集合中的對象不會按特定的方式排序,它只是簡單地把對象放到集合中。
從特性上來看,Set相當于是一個只存儲key、不存儲value的Map。我們可以把Set想象成是一個”特殊的Map“,這個Map只有key卻沒有value,所以我們可以用Set去除重復的元素。另外由于放入Set的元素和Map的key類似,需要正確地實現equals()和hashCode()方法,否則該元素就無法正確地放入Set。
2.Set特性
與其他集合不同,Set集合具有自己的一些特性:
● Set集合中的元素都是唯一的,不允許有重復值,且最多只允許包含一個null元素;
● Set集合中的元素沒有順序,我們無法通過索引來訪問元素,但TreeSet是有序的;
● Set集合沒有固定的大小限制,可以動態地添加和刪除元素;
● Set集合提供了高效的元素查找和判斷方法。
3.Set常用方法
Set集合給我們提供了一系列常用的方法,用于添加、刪除、查找、遍歷和獲取集合元素等操作,下面是Set集合中常用方法的實現過程。
3.1 添加元素
我們可以使用add()方法進行元素的添加。
public boolean add(E e)
該方法用于向Set集合添加元素,如果元素已經存在,則不會添加;如果添加成功,則返回true,否則返回false。該方法的示例代碼如下:
Set<String> set = new HashSet<>();
set.add("hello word");
set.add("java");
set.add("iOS");
System.out.println(set);
3.2 刪除元素
我們可以使用remove()方法進行元素的刪除。
public boolean remove(Object o)
該方法用于從Set集合中刪除指定的元素。如果元素存在且刪除成功,則返回true,否則返回false。該方法的示例代碼如下:
Set<String> set = new HashSet<>();
set.add("hello word");
set.add("java");
set.remove("java");
System.out.println(set); // 輸出結果為:[壹小編]
3.3 判斷元素
我們可以使用contains()方法進行元素的判斷。
public boolean contains(Object o)該方法用于判斷Set集合中是否包含指定的元素。如果元素存在,則返回true,否則返回false。該方法的示例代碼如下:
Set<String> set = new HashSet<>();
set.add("hello word");
set.add("java");
System.out.println(set.contains("java")); // 輸出結果為:true
System.out.println(set.contains("orange")); // 輸出結果為:false
3.4 獲取元素數量
我們可以使用size()方法判斷集合的數量。
public int size()
該方法的使用示例代碼如下:
Set<String> set = new HashSet<>();
set.add("hello word");
set.add("java");
System.out.println(set.size()); // 輸出結果為:2
二. HashSet集合
1.簡介
在Java的集合框架中,HashSet是一種非常常用的集合類型,它實現了Set接口,并繼承了AbstractSet抽象類。HashSet集合的底層實現是一個哈希表,它使用哈希算法來存儲和管理集合中的元素。HashSet集合中的元素沒有順序,且不允許重復。
如果我們想使用HashSet集合,一般要使用如下兩個構造方法創建出HashSet對象:
● HashSet():構造一個新的空的Set集合對象;
● HashSet(Collection c):構造一個包含指定Collection集合元素的新Set集合。"< >"中的extends,表示這個Collection中的元素必須繼承自HashSet的父類,該部分限定了Collection元素的類型。
2.HashSet特性
HashSet作為Set集合的具體子類,具有以下特點:
● HashSet的底層是基于HashMap來實現的;
● HashSet中的元素是唯一的,內部不允許有重復的元素;
● 無序,不會記錄插入元素的順序,所以不能保證元素的排列順序,獲取順序可能與添加順序不同;
● HashSet集合沒有固定的大小限制,可以動態地添加和刪除元素;
● HashSet集合中的元素最多可以有一個null值;
● HashSet不是線程安全的,默認線程不同步,如果有多個線程同時訪問或修改同一個HashSet,必須通過代碼來保證同步操作。
3.去重原理
從底層實現來看,HashSet的底層其實就是一個值為Object的HashMap,如下圖所示:

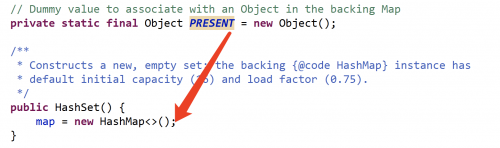
所以HashSet其實就是按照Hash算法來實現元素的查找和存儲的,具有很好的存取和查找性能。當我們向HashSet集合中存入一個元素時,HashSet會調用該對象的hashCode()方法來得到該對象的hashCode值,然后根據該hashCode值決定該對象在HashSet中的存儲位置。此時如果有兩個元素通過equals()方法進行比較,返回的結果為true,但它們的hashCode卻不相等,HashSet也會把它們存儲在不同的位置,我們依然可以添加成功。也就是說,如果兩個對象的hashCode值相等,且通過equals()方法比較返回的結果也為true, HashSet集合才會認為兩個元素相等。
4.使用案例
我們通過一個簡單的案例,來看看HashSet的基本用法。
import java.util.HashSet;
public class Demo11 {
public static void main(String[] args) {
//創建HashSet集合
HashSet<String> set = new HashSet<String>();
set.add("java");
//重復元素無法被添加進去
set.add("java");
System.out.println(set);
//集合遍歷
Iterator<String> it = set.iterator();
while (it.hasNext()) {
//輸出Set集合中的每個元素
System.out.println("值="+it.next());
}
}
}
在上面的代碼中,我們通過HashSet的構造方法創建了一個Set集合對象,并將幾個元素對象存儲到了這個Set集合中。然后我們使用HashSet類中的iterator()方法獲取一個Iterator對象,并調用hasNext()方法遍歷集合元素,再使用next()方法獲取到下一個數據元素。但是HashSet輸出的元素是無序的,輸出時既不是添加元素的順序,也不是String排序的順序,在不同版本的JDK中,這個順序可能也是不同的。另外因為Set是不可重復的,如果我們向Set集合中添加了兩個相同的元素,則后添加的會覆蓋前面添加的元素,所以Set集合中不會出現相同的元素。
三. TreeSet集合
1.簡介
TreeSet是一種很常用的集合類型,它實現了Set和SortedSet接口,并且繼承自AbstractSet抽象類。TreeSet集合中的元素也是唯一的,不允許重復。TreeSet集合的底層基于紅黑樹,可以使用自然排序或指定的比較器對集合中的元素進行排序。該類具有如下特點:
● TreeSet集合中的元素是唯一的,不允許重復。
● TreeSet集合中的元素是有序的,因為實現了SortedSet接口,具有字典順序,可以通過迭代器按照升序或降序遍歷。
● TreeSet集合沒有固定的大小限制,可以動態地添加和刪除元素。
● TreeSet集合提供了高效的元素查找和判斷功能。
另外,SortedSet接口是Set接口的子接口,能夠對集合進行自然排序,因此TreeSet類默認情況下就是自然排序(升序)的。但TreeSet只能對實現了Comparable接口的類對象進行排序,所以我們使用TreeSet集合存儲對象時,該對象必須要實現Comparable接口。這是因為Comparable接口中有一個compareTo(Object o)方法,可以比較兩個對象的大小。例如,a.compareTo(b),如果 a 和 b 相等,則該方法會返回 0;如果 a 大于 b,則該方法返回大于 0 的正值;如果 a 小于 b,則該方法返回小于 0 的負值。
2.常用方法
除了Set類中通用的方法之外,TreeSet類還有如下幾個特有的方法:
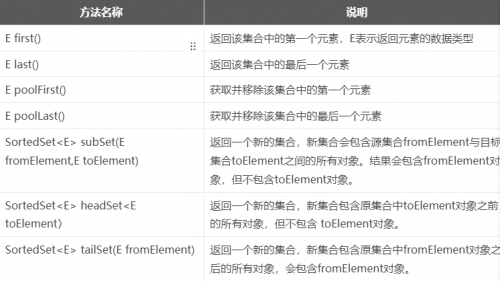
因為TreeSet中的元素是有序的,所以增加了訪問第一個、前一個、后一個、最后一個元素的相關方法,并提供了3個從 TreeSet中截取子TreeSet的方法。
3.去重原理
當TreeSet集合在保存對象元素時,集合對象必須實現Comparable接口,并重寫compareTo方法,該方法有如下兩個作用:
● 排序: 返回值大于0表示升序,返回值小于0表示降序;
● 去重(返回值為0):TreeSet認為返回0,表示兩個對象是相同的對象。
所以我們利用TreeSet實現去重的原理就是:如果compareTo()方法的返回值為0,則認為是相同的對象;如果compareTo()方法的返回大于0,則是升序排序;如果小于0,則是降序排序。
4.使用案例
接下來我們再通過一個案例來看看TreeSet的用法。
4.1 編寫Person類
首先我們設計一個Person類,該類要實現Comparable接口。當TreeSet集合在保存對象元素時,集合中添加的元素對象必須實現Comparable接口,并重寫compareTo方法。如果沒有實現Comparable接口,那么創建TreeSet時必須傳入一個Comparator對象。
/**
* 實現Comparable接口,并重新compareTo()方法
*/
public class Person implements Comparable<Person>{
private String username;
private String password;
public Person() {
}
public Person(String username, String password) {
super();
this.username = username;
this.password = password;
}
@Override
public String toString() {
return "User [username=" + username + ", password=" + password + "]";
}
//重寫compareTo()方法,對Person對象進行比較
@Override
public int compareTo(Person o) {
if(!this.username.equals(o.username)) {
//根據姓名及長度進行比較
return this.username.length() - o.username.length();
}else {
//根據密碼進行比較
if(this.password.equals(o.password)) {
return 0;
}else {
//比較姓名的長度
return this.username.length() - o.username.length();
}
}
}
}
4.2 測試TreeSet排序功能
然后我們往TreeSet集合中添加若干個對象元素進行排序測試,代碼如下:
import java.util.TreeSet;
public class Demo12 {
public static void main(String[] args) {
//TreeSet的去重原理
TreeSet<Person> set = new TreeSet<Person>();
set.add(new Person("admin","123"));
set.add(new Person("yyg","bb"));
set.add(new Person("jack","123"));
set.add(new Person("rose123","123"));
set.add(new Person("admin","123"));
set.add(new Person("xksss6","abc"));
//如果兩個對象的用戶名和密碼都相等,則認為是兩個相同的對象,且按照名字長度升序存放
for (Person person : set) {
System.out.println(person);
}
}
}
我們在遍歷TreeSet時,輸出的元素是有序的,這個順序是元素的排序順序。但是我們在使用TreeSet進行自然排序時,只能向 TreeSet 集合中添加相同數據類型的對象,否則會拋出 ClassCastException異常。如果向 TreeSet集合中添加了一個 Double類型的對象,則后面只能添加 Double對象,不能再添加其他類型的對象,例如 String對象等。
四. 結語
至此,小編就帶各位把Set集合及其子類學習完了,現在你學會了嗎?本文的重點內容如下所示:
● Set用于存儲不重復的元素集合;
● 放入HashSet的元素,與作為HashMap的key要求相同;
● 放入TreeSet的元素,與作為TreeMap的Key要求相同;
● 利用Set可以去除重復元素;
● 遍歷SortedSet時,可以按照元素的排序順序進行遍歷,我們也可以自定義排序算法;





















 京公網安備 11010802030320號
京公網安備 11010802030320號