1.概念

　　首先我們得知道進制的概念。所謂的進制，也叫做進位計數制，這是人為定義的帶進位的計數方法。當然也有不帶進位的計數方法，比如原始的結繩計數法，唱票時常用的“正”字計數法等。

　　任何一種進制，每一位上的數在運算時都是滿X進一位。比如十進制是逢十進一，十六進制是逢十六進一，二進制就是逢二進一，以此類推，X進制就是逢X進1位。以我們最熟悉的十進制為例，每逢十進一，當數為19時，下一位數的尾數便滿足該進制的最大數，于是下一位末位清零，前置位+1，變成20。

　　2.分類

　　在計算機中，目前常用的進制有如下幾種：

　　●十進制;

　　●二進制;

　　●八進制;

　　●十六進制

　　因為在計算機的底層只能處理二進制格式的數據，也就是0和1，其他的文字、數字、字符等信息都要轉換成二進制的格式，計算機的底層才能識別處理。所以作為一個程序員，二進制是我們必須要理解和掌握的哦。

　　3. 二進制

　　作為一個程序員，必須要掌握的進制就是二進制了，其實我們只需要參考十進制就可以很容易理解進制的問題了。所謂的二進制，里面只有0和1，且滿二進一，所以在二進制里是看不到>=2的數的。比如二進制的前10位數分別是0、1、10、11、100、101、110、111、1000、1001。

　　4. 八進制

　　八進制中有07共8個數字，但沒有8哦，其規則是滿八進一，所以7的下一位數不是8，而是10。17的下一位數不是18，而是20。比如八進制的前10位數分別是0、1、2、3、4、5、6、7、10、11......

　　5. 十六進制

　　十六進制中有0F共16個數字，同樣沒有16，其規則是滿十六進一。在十六進制中，這16個數字分別是0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F。即9的下一位不是10，而是A，10這個數只是十進制的衍生物，這一點大家要注意!

　　同理，在十六進制中，19的下一位不是20，而是1A，1F的下一位才是20;99的下一位是9A，FF的下一位才是100。

　　6. 原碼、反碼與補碼

　　6.1 原碼

　　對一個正整數來說，所謂的原碼，就是指一個整數對應的二進制，比如整數10的原碼就是00001010。所以原碼就是一個正整數原本對應的二進制形式。但負數的原碼和正數卻不一樣，負數的原碼要將正數原碼的符號位(最高位)改為1，比如-10的原碼就是10001010。

　　6.2 反碼

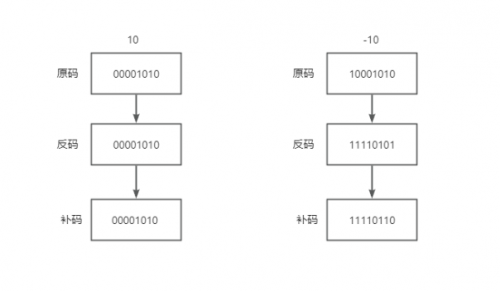
　　正數的反碼就是其原碼，即正數的原碼和反碼完全相同。而負數的反碼則是將原碼中除符號位以外的所有位(數值位)都取反，即 0 變成 1，1 變成 0。如10的原碼和反碼都是00001010，而-10的原碼是10001010，反碼則是11110101。

　　6.3 補碼

　　正數的補碼就是其原碼，所以正數的原碼、反碼、補碼都相同。而負數的補碼是其反碼加1，-10的原碼是10001010，反碼則是11110101，補碼則是11110110。我們可以認為，補碼是在反碼的基礎上打了一個補丁，進行了一點修正，所以叫做“補碼”。

　　所以原碼、反碼、補碼的概念只對負數有實際意義，對于正數來說，原碼、反碼、補碼其實都是一樣的，如下圖所示：

　　7.作用

　　在Java中，進制轉換可以用來在不同的進制之間轉換數字。以下是一些進制轉換的應用：

　　1.二進制和十六進制是計算機中常用的數字表示方法。轉換為這些進制可以方便地表示和處理二進制和十六進制數據。

　　2.進制轉換也是密碼學中的重要概念。例如，在加密和解密過程中，需要將數字轉換為不同的進制，以實現安全傳輸和存儲。

　　3.在算法和數據結構中，進制轉換也很常見。例如，將一個數字轉換為二進制可以方便地實現位運算，這在許多算法中都有用。

　　4.進制轉換還可以用于顯示數字。例如，在編寫計算機程序時，需要將數字轉換為字符串，并以不同的進制進行顯示。

　　5.進制轉換是計算機科學的基礎知識之一，對于理解計算機的工作原理也是很有幫助的。