一、最小二乘法概念與用途知悉

最小二乘法是一種常用的數學方法，用于通過擬合數據點來找到最佳擬合曲線或平面。其核心思想是最小化觀測數據點與擬合曲線之間的垂直距離的平方和，即最小化殘差的平方和。通過最小二乘法，我們可以找到一條曲線或平面，使得觀測數據點到該曲線或平面的距離最短。

最小二乘法廣泛應用于各個領域，尤其在數據擬合和回歸分析中。例如，在線性回歸中，最小二乘法可以用來擬合數據集到一條直線;在多項式擬合中，最小二乘法可以用來擬合數據集到一個多項式曲線;在非線性擬合中，可以通過最小二乘法找到最佳擬合曲線或曲面。

通過最小二乘法，我們可以得到擬合曲線的參數，如斜率和截距，或者擬合曲面的系數。這些參數可以用來進行預測、優化和分析數據。最小二乘法的優點在于可解析解的存在，計算較為簡單和穩定。

二、舉例詳解

舉個通俗的例子，某種材料的強度與其拉伸倍數有關，現有一部分樣品的測試數據：

將上述數據畫成如下圖形，假設我們想用一條直線來擬合數據，即期望找到一條直線能最好的穿過這些數據點。

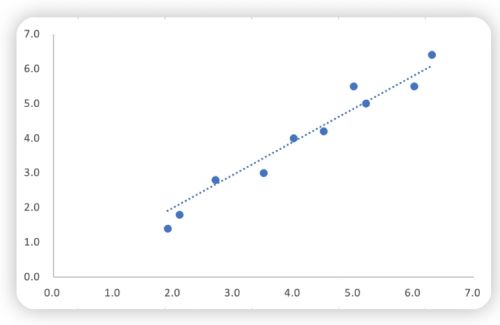
通過觀察可以發現，這些點大致分布在一條直線上，因此可以考慮利用一元二次方程：

當然，事物總具有兩面性，最小二乘法也不例外，最小二乘法不夠穩健，很容易受極端異常點的影響，如果是少數異常，可以用異常點檢測的方法剔除，但有時異常點也非常重要，需要考慮，這時候可以用一些穩健的方法，具體可以搜索“穩健回歸”，找相關的文獻看看，或者等待作者后續更新。