01舉個例子
在生活中,身高是一個常見的連續變量,而且大多數人的身高分布符合正態分布。例如,假設我們測量了一個班級中所有學生的身高,并畫出了身高的頻率分布直方圖。如果這個分布呈現出鐘形曲線的形狀,那么這個分布就可以被認為是正態分布。在正態分布中,大多數人的身高會集中在中間,而極端的高或低身高的人數則較少。
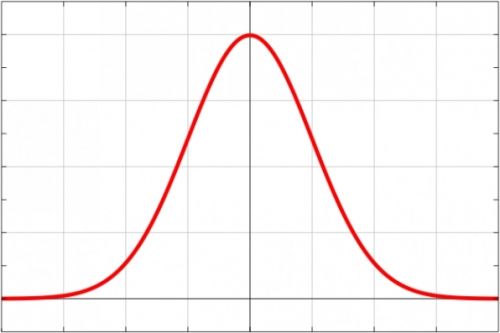
正態分布是統計學中常用的一種分布類型,它也被稱為高斯分布或鐘形曲線。正態分布的特點是具有單峰、對稱、連續和無限可分性等特點。它的概率密度函數具有一個峰值,峰值處的概率最大,并且在峰值兩側逐漸減小,呈現出一條平滑的鐘形曲線。正態分布在生活中和數據分析工作中都有廣泛的應用。
02為什么會出現正態分布?
正態分布是一種統計學上的概率分布模型,它是自然界和社會現象中最常見的分布之一。從自然界規律的角度來解釋這種現象,我們可以從以下幾個方面進行闡述:
中心極限定理
中心極限定理是統計學中的一個基本定理,它指出當樣本量足夠大時,任何隨機變量的均值分布將趨近于正態分布。這個定理可以解釋為,在自然界和社會現象中,許多現象是由許多不同因素的綜合作用而形成的,這些因素的影響是隨機的,而且通常是相互獨立的。因此,隨著數據量的增加,這些隨機因素的影響將趨于平均化,產生一個近似正態分布的結果。
自然界的復雜性
自然界中的許多生物和物種都具有復雜的生理和行為特征。例如,身高、體重和壽命等生物學變量通常受到許多基因和環境因素的影響。由于這些因素的影響是隨機的,它們可能會產生一個接近正態分布的結果。
人類社會的復雜性
人類社會和經濟活動也具有相當的復雜性。例如,收入、財富和教育水平等變量通常受到許多社會、文化和經濟因素的影響。這些因素的影響通常是隨機的,并且可能在不同的群體之間呈現出正態分布的形式。
所以,正態分布在自然界和社會現象中非常常見,這是由于許多因素的隨機性和獨立性作用于復雜的生物、自然和社會系統而產生的結果。
03數分中正態分布使用場景
在數據分析工作中,正態分布是非常重要的概念,因為它可以幫助我們判斷數據是否符合某些假設,以及確定使用哪種統計方法。以下是一些數據分析工作中需要使用正態分布的場景:
假設檢驗
在假設檢驗中,我們需要假設數據是從一個已知分布中隨機抽取的。如果我們假設數據來自正態分布,那么就需要檢驗數據是否符合正態分布。許多假設檢驗的方法都基于正態分布的假設。例如,當我們需要檢驗兩個樣本的平均值是否相等時,我們可以使用t檢驗。但是,t檢驗的前提條件是樣本符合正態分布。如果數據不符合正態分布,則需要使用非參數檢驗方法。
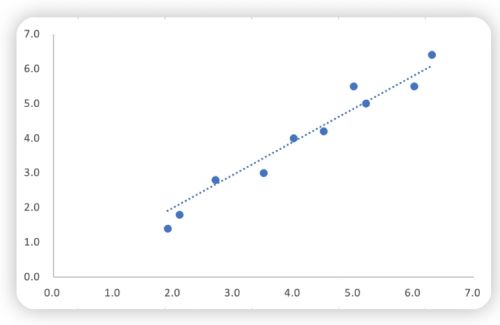
回歸分析
在回歸分析中,我們通常假設因變量在各自的自變量取值下是正態分布的。如果數據不符合正態分布,我們可能需要對數據進行轉換,使其更符合正態分布。
統計建模
在許多統計建模中,我們需要假設響應變量(例如銷售額)的分布符合正態分布。如果響應變量不符合正態分布,則需要采用其他建模方法,例如廣義線性模型或非參數方法。
控制圖
控制圖是一種質量控制工具,可以幫助我們監控過程是否處于控制狀態。控制圖中的控制限也是基于正態分布的假設計算出來的。
04數分中正確使用正態分布
在數據分析中,正確使用正態分布可以幫助我們做出更準確和可靠的統計推斷。以下是一些使用正態分布的建議:
正態性檢驗
在使用正態分布進行假設檢驗或模型構建之前,需要先進行正態性檢驗以確保數據符合正態分布。
繪制直方圖或密度圖:繪制直方圖或密度圖可以幫助我們觀察數據的分布情況,并判斷是否符合正態分布。如果數據呈現出鐘形曲線的形狀,那么它很可能是正態分布。
使用相關工具和技術:在數據分析中,有許多工具和技術可以幫助我們使用正態分布進行分析,例如正態分布表、正態概率圖、Q-Q圖等。
進行正態性檢驗:進行正態性檢驗可以幫助我們確定數據是否符合正態分布。在數據分析中,有很多方法可以檢驗數據的正態性,例如Shapiro-Wilk檢驗、Kolmogorov-Smirnov檢驗、Anderson-Darling檢驗等。但需要注意的是,即使正態性檢驗的結果顯示數據不符合正態分布,也不一定意味著我們不能使用基于正態分布的方法,因為有些方法對數據分布的偏離并不敏感。
正態性變換
如果數據不符合正態分布,我們可以嘗試對數據進行變換,使其更接近于正態分布。例如,可以嘗試對數變換、平方根變換或Box-Cox變換等。
理解正態分布的性質
正確理解正態分布的性質,在進行統計分析時,了解正態分布的性質可以幫助我們更好地理解數據。例如,正態分布有一個平均值和標準差,這些統計量可以用來描述數據的中心和變異程度。在進行假設檢驗或建模時,我們需要知道正態分布的均值和標準差的性質,以便進行正確的統計推斷。
正態分布與抽樣誤差
正確理解正態分布與抽樣誤差的關系,在數據分析中,我們通常會從樣本中進行推斷整個總體的性質。正態分布與中心極限定理的關系,可以幫助我們理解樣本大小對抽樣誤差的影響。如果樣本足夠大,即使總體不符合正態分布,樣本均值的分布也會趨近于正態分布。
謹慎使用
雖然正態分布在許多情況下非常有用,但并不是所有數據都符合正態分布。在使用正態分布時,需要注意數據的特征,以便確定是否適用于該分布。
05總結
總之,正態分布是數據分析中非常重要的概念,它可以幫助我們判斷數據是否符合某些假設,以及確定使用哪種統計方法。在數據分析工作中,我們需要正確理解和使用正態分布,以避免誤解數據分布和誤用統計方法。



















 京公網安備 11010802030320號
京公網安備 11010802030320號